Métodos Computacionais no Ensino da Física

1.13 Exercícios

Exercício 1.13.1

Se você conseguiu montar a sua própria planilha seguindo os passos detalhados nesta aula, você está preparado para o estudo independente de outros aspectos da termodinâmica do gás ideal. Em especial, você deve conseguir, com facilidade, estudar outras classes de transformações.

Uma classe de transformações comumente considerada é a transformação adiabática, o que significa simplesmente que não há troca de calor entre o gás e o meio ambiente, ou ainda, q=0. Esse é o assunto que é proposto como exercício. Serão dadas apenas algumas indicações:

• Crie mais duas planilhas, clones de Isotérmica 1 e Isotérmica 2, no arquivo que você já tem. Chame-as Adiabática 1 e Adiabática 2.
• Adapte essas planilhas ao caso particular de transformações adiabáticas. Como no caso das transformações isotérmicas, considere duas transformações que diferem apenas pelo valor da pressão inicial (mesmos valores para o volume inicial e para a temperatura inicial). É interessante considerar uma expansão adiabática, portanto valores relativamente altos da pressão inicial e um valor de w negativo. Utilize o mesmo valor de w para ambas as transformações.
• Veja como ficam as linhas de tendência no diagrama p-V. Era o que você esperava? Justifique.
• Insira um segundo diagrama, agora do tipo T-V. Para facilitar, você pode selecionar o gráfico p-V que você já tem e fazer Copiar-Colar para criar um clone, no qual você pode fazer as modificações necessárias para transformá-lo num gráfico T-V.
• Como ficam as linhas de tendência no diagrama T-V? Era o que você esperava? Justifique.

Exercício 1.13.2

Neste exercício você irá analisar, inicialmente, um oscilador linear na ausência de força resistiva e de força externa e, depois, o problema de um oscilador linear em um meio resistivo. [Trata-se de um problema que pode ser formulado no quadro de uma disciplina de Física de um curso de Física Geral universitária ou até mesmo do Ensino Médio com as devidas simplificações.] Começa-se por revisar os princípios e relações relevantes.

Será estudado o movimento unidimensional de um sistema massa-mola, exemplo típico para o estudo de osciladores, constituído por um corpo de massa m, que desliza sobre uma superfície lisa, ligado a uma mola de constante de força (ou constante elástica) k. Na Figura 1.13.1 é apresentado um sistema massa-mola, onde são mostradas duas situações, o sistema massa-mola na posição de equilíbrio (no topo da figura) e em uma posição deslocada, à direita da posição de equilíbrio, movendo-se com uma velocidade orientada para a direita. A força restauradora exercida pela mola sobre o corpo (F), uma força resistiva que representa a presença de um meio viscoso (F_resistiva) e uma força externa (F_externa) também estão assinaladas na figura.

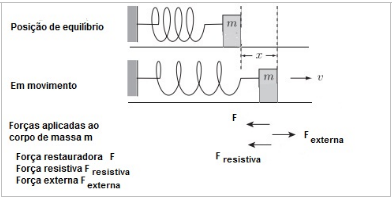
Na ausência de um meio viscoso e de uma força externa aplicada e considerando-se uma força restauradora linear, a mola exerce uma força F = - k x sobre o corpo de massa m. A equação de movimento do corpo (2^a Lei de Newton) é dada por:

A solução dessa equação diferencial ordinária de segunda ordem pode ser expressa de várias formas. A solução proposta aqui é do tipo:

onde A e B são duas constantes a serem determinadas quando da análise do problema físico com suas condições iniciais: a posição inicial, x(t=0) = x₀, e a velocidade inicial dx/dt(t=0) = v(t=0) = v₀, . A quantidade ω₀ é a frequência natural do oscilador e é dada por ω₀² = k / m, como pode ser verificado substituindo-se a solução proposta na equação de movimento.

O cálculo da velocidade e da aceleração do bloco como funções do tempo fornece:

Na presença de um meio viscoso, em que a força que é aplicada à massa m é do tipo linear na velocidade: F_resistiva = - b v = - b (dx/dt), o corpo de massa m estará sob ação da resultante das forças a ele aplicadas: F_resultante = F_restauradora + F_resistiva, sendo então F_resultante = - k x - b (dx/dt) a força resultante. Como d²x/dt² = F_resultante / m, e definindo-se o parâmetro 2β = b / m , a equação de movimento pode ser escrita como:

No caso de um amortecimento fraco a solução ainda é oscilatória e o oscilador é dito subamortecido. Isto ocorre quando β² < ω₀² - o parâmetro β, que mede o amortecimento, é pequeno em relação à frequência natural do oscilador ω₀. Define-se, então, um parâmetro ω₁² = ω₀² - β², fazendo com que a solução seja do tipo:

A partir da solução x (t), pode-se facilmente encontrar as expressões para a velocidade e para a aceleração como funções do tempo. Para o cálculo da velocidade, basta derivar a expressão (1.13.5) em relação ao tempo, e para a aceleração do bloco, deriva-se x(t) duas vezes em relação ao tempo:

e

Exercício 1.13.2.a

Inicialmente será analisado o caso mais simples do oscilador linear sem amortecimento.

Considere um oscilador que se encontra na posição x₀ com vetor velocidade de intensidade v₀ e orientado da esquerda para a direita. Determine a posição, a velocidade e a aceleração do oscilador como funções do tempo, x(t), v(t) e a(t).

Com essas condições iniciais, [x(t=0) = x₀ e v(t=0) = v₀], se obtém: x(t=0) = x₀ = A cos(0) + B sen(0) = A e v(t=0) = v₀ = ω₀ [- A sen(0) + B cos(0)] = ω₀ B. Assim, os coeficientes de x(t) (Equação 1.13.2) são: A = x₀ e B = v₀ / ω₀, obtendo-se:

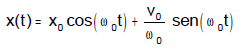Consulte o material das seções deste capítulo, que mostra através de um tutorial os procedimentos básicos a serem seguidos quando se deseja usar a planilha eletrônica para analisar o comportamento de grandezas físicas associadas a um problema-exemplo. Entre esses podem ser citados: (i) salvar sua planilha e dar-lhe um nome; (ii) identificar as células da planilha; (iii) fazer a mesclagem de células; (iv) escrever fórmulas para análise de grandezas incluindo dados presentes em células; (v) identificar conteúdos de células que permanecem fixos; (vi) incluir notas explicativas; (vii) realizar manipulação a partir de expressão digitada em certa célula para gerar os valores sucessivos em células vizinhas na mesma linha ou na mesma coluna; (viii) construir gráficos.

Abra a planilha eletrônica (Excel ou Calc do BrOffice). Escolha um título para nomear seu trabalho com o oscilador harmônico simples. Para esse problema-exemplo, os dados podem ser classificados como parâmetros (a massa do bloco m e a constante elástica da mola k); e condições iniciais (a posição e a velocidade do objeto). Será conveniente organizar esses dados em colunas. Inclua as unidades correspondentes no sistema internacional.

Ao final deste exercício, você terá construído uma planilha que calcula a posição, a velocidade e a aceleração de um oscilador harmônico simples como funções do tempo e terá construído os gráficos correspondentes. Você poderá analisar o comportamento de seus gráficos em decorrência da alteração dos dados de entrada. A sugestão é que você mantenha fixo o valor da massa do bloco m.

1. Altere o valor da constante elástica da mola, k analise as modificações resultantes nos gráficos.
2. Você, agora, alterará os valores da posição e da velocidade inicial do bloco, tomando o cuidado de incluir valores compatíveis com o problema físico.

Exercício 1.13.2.b

Agora você analisará a situação de um oscilador harmônico subamortecido. Em uma planilha, introduza os parâmetros correspondentes a esse oscilador e as expressões para a posição, a velocidade e a aceleração como funções do tempo (ver as Equações 1.13.5 a 1.13.7). Você construirá os gráficos da posição, da velocidade e da aceleração versus o tempo para esse oscilador.

Considere um oscilador em um meio resistivo que, em t=0, se encontra na posição x₀ com velocidade v₀. Determine a posição, a velocidade e a aceleração do oscilador como funções do tempo, x(t), v(t) e a(t).

Com as condições iniciais ([x(t=0) = x₀ e v(t=0) = v₀]) se obtém: x(t=0) = x₀ = A e v(t=0) = v₀ = - βA + ω₁ B. Ou seja, B = (v₀ + βx₀) / ω₁, onde ω₁² = ω₀² - β².

Os procedimentos a serem seguidos são similares àqueles adotados no exercício 1.13.2.a. Para esse problema exemplo, oscilador sub-amortecido, os parâmetros são a massa do bloco m, a constante elástica da mola k, e sugere-se utilizar β como parâmetroassociado à força resistiva; as condições iniciais são a posição e a velocidade, como no exercício anterior.

Ao final deste exercício você terá construído uma planilha que calcula a posição, a velocidade e a aceleração de um oscilador harmônico subamortecido como funções do tempo e terá construído os gráficos correspondentes. Você poderá analisar o comportamento de seus gráficos em decorrência da alteração dos dados de entrada. Como no exercício anterior, mantenha fixo o valor da massa do bloco, m.

1. Altere o valor da constante elástica da mola k e veja como isto altera os gráficos.
2. Você deverá analisar o comportamento dos seus gráficos frente a modificações do parâmetro β. Para tal, mantenha fixo o valor de k e altere agora o valor de β. Não esqueça que o parâmetro β deve ser mantido menor que ω₀, pois se está trabalhando com um oscilador subamortecido!
3. Você alterará, agora, os valores da posição e da velocidade inicial do bloco, tomando o cuidado de incluir valores compatíveis com o problema físico.