!DOCTYPE HTML PUBLIC "-//IETF//DTD HTML 3.2//PT"> Trigonometria Esferica

FIS02016 - Astronomia de Posição - Profa. Maria de Fátima O. Saraiva

Trigonometria Esférica

A astronomia esférica, ou astronomia de posição, diz respeito fundamentalmente às direções na qual os astros são vistos, sem se preocupar com sua distância. É conveniente expressar essas direções em termos das posições sobre a superfície de uma esfera - a Esfera Celeste. Essas posições são medidas unicamente em ângulos. Dessa forma, o raio da esfera, que é totalmente arbitrário, nõ entra nas equações.

Definições básicas:

Se um plano passa pelo centro de uma esfera, ele a dividirá em dois hemisférios idênticos, ao longo de um grande círculo, ou círculo máximo. Qualquer plano que corta a esfera sem passar pelo seu centro a intercepta em um círculo menor ou pequeno.

Quando dois círculos máximos se interceptam em um ponto, formam entre si um ângulo esférico. A medida de um ângulo esférico é igual á medida do ângulo plano entre as tangentes dos dois arcos que o formam.

Um ângulo esférico também é medido pelo arco esférico correspondente, que é o arco de um círculo máximo contido entre os dois lados do ângulo esférico e distantes 90 de seu vértice. A medida de um arco esférico, por sua vez, é igual ao ângulo que ele subentende no centro da circunferência.

Triângulos esféricos:

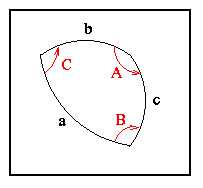
Um triângulo esférico não é qualquer figura de três lados sobre a esfera; seus lados devem ser arcos de grandes círculos, ou seja, arcos esféricos. Denotamos os ângulos de um triângulo esférico por letras maiúsculas (A,B,C), e os seus lados por letras minúsculas (a,b,c).

Propriedades dos triângulos esféricos

1) A soma dos ângulos de um triângulo esférico é sempre maior que 180° e menor do que 540° e não é constante, dependendo do triângulo. De fato, o excesso a 180° é diretamente proporcional à área do triângulo.

2) A soma dos lados de um triângulos esférico é maior do que zero e menor do que 360°.

3) Os lados maiores estão opostos aos ângulos maiores no triângulo.

4) A soma de dois lados do triângulo é sempre maior do que o terceiro lado, e a diferença é sempre menor.

5) Cada um dos lados do triângulo é menor do que 180°, e isso se aplica também aos ângulos.

Solução de triângulos esféricos:

Ao contrário da trigonometria plana, não é suficiente conhecer dois ângulos para resolver o triângulo esférico. É sempre necessário conhecer no mínimo três elementos: ou três ângulos, ou três lados, ou dois lados e um ângulo, ou um ângulo e dois lados.

As fórmulas principais para a solução dos triângulos esféricos são:

lei dos cossenos para os lados:

cos a = cos b cos c + sen b sen c cos A (1)
cos b = cos a cos c + sen a sen c cos B (2)
cos c = cos a cos b + sen a sen b cos C,

a lei dos cossenos para os ângulos:

cos A = - cos B cos C + sen B sen C cos a
cos B = - cos A cos C + sen A sen C cos b
cos C = - cos A cos B + sen A sen B cos c

e a lei dos senos:

sen a / sen A = sen b / sen B = sen c / sen C

Uma dedução dessas fórmulas pode ser vista, por exemplo, em www.if.ufrgs.br/oei/santiago/fis2005/textos/esferast.htm.

Uma outra relação que pode ser bastante útil em muitos casos é obtida substituindo a lei dos cossenos para um lado na lei dos cossenos para o outro, como deduzimos a seguir:

Escrevendo a (2) como;

sen c sen a cosB = cos b - cos c cos a (3)

Substituindo a (1) na (3):

sen c sen a cos B = cos b - cos c (cos b cos c + sen b sen c cos A) = cos b - cos²c cos b - sen b senc cos c cos A = cos b (1 - cos²c) - sen b sen c cos c cos A = cos b sen² c - sen b sen c cos c cos A

Dividindo por sen c, temos a fórmula dos 5 elementos ;

sen a cos B = sen c cos b - sen b cos c cos A

Essa fórmula é a única que relaciona 5 elementos (três lados e dois ângulos), e tem a vantagem de resolver ambiguidades de sinal.

Aplicação:Determinação da distância angular entre estrelas

A separação angular entre duas estrelas é a distância medida ao longo do círculo máximo passando pelas duas estrelas. Sejam A e B as duas estrelas, e sejam α_A, δ_A, α_B, δ_B, as suas coordenadas.

Podemos construir um triângulo esférico em que um dos lados seja a separação angular entre elas e os outros dois lados sejam as suas distâncias polares, ou seja, os arcos ao longo dos meridianos das estrelas desde o pólo () até as estrelas.

Pela fórmula dos cossenos temos:

$cos\widehat{AB} = cos\widehat{PA} ...sen\widehat{PB} cos\widehat{APB}$

Onde:

$\widehat{AB} = distancia polar entre A e B$

$\widehat{PA} = distancia polar de A = 90^\circ - \delta_A$

$\widehat{PB}=distancia polar de B = 90^\circ - \delta_B$

$\widehat{APB}=angulo entre o meridiano de A e o meridiano de B = \alpha_A - \alpha_B$

E portanto:

$cos\widehat{PA}=sen\delta_A$

$cos\widehat{PB}=sen\delta_B$

$sen\widehat{PA}=cos\delta_A$

$sen\widehat{PB}=cos\delta_B$

$cos\widehat{APB}=cos(\alpha_A-\alpha_B)}$

E finalmente:

$cos\widehat{AB}=sen\delta_A ...cos\delta_B cos(\alpha_A-\alpha_B)$

Exemplo:

Qual o tamanho da constelação do Cruzeiro do Sul, medido pelo eixo maior da Cruz?

O eixo maior da Cruz é formado pelas estrelas Gacrux ( $\alpha = 12h\,31m\,11s$ = $\delta = -57^\circ\,07^\prime$ ) e Acrux ( $\alpha = 12h\,26m\,37s$ ; $\delta = -63^\circ\,06^\prime$ )

Chamando o tamanho do eixo maior da Cruz, e aplicando a equação acima, temos:

$cos D= sen\delta_{Gacrux} sen ...a_{Acrux} cos(\alpha_{Gacrux}-\alpha_{Acrux})}$

$\delta_{Gacrux}= -57^\circ\,07^\prime= -57,11^\circ$

$\alpha_{Gacrux} = 12h\,31m\,11s = 187,80^\circ$

$\delta_{Acrux} = -63^\circ\,06^\prime= -63,10^\circ$

$\alpha_{Acrux} = 12h\,26m\,37s = 186,65^\circ$

Substituindo esses valores na equação temos:

$cos D= {sen(-57,11^\circ)}sen ... (-63,10^\circ)} cos (187,80^\circ - 186,65^\circ)$

Portanto:

$cos D= 0,9945 \Rightarrow D = 6^\circ$

O Triângulo de Posição

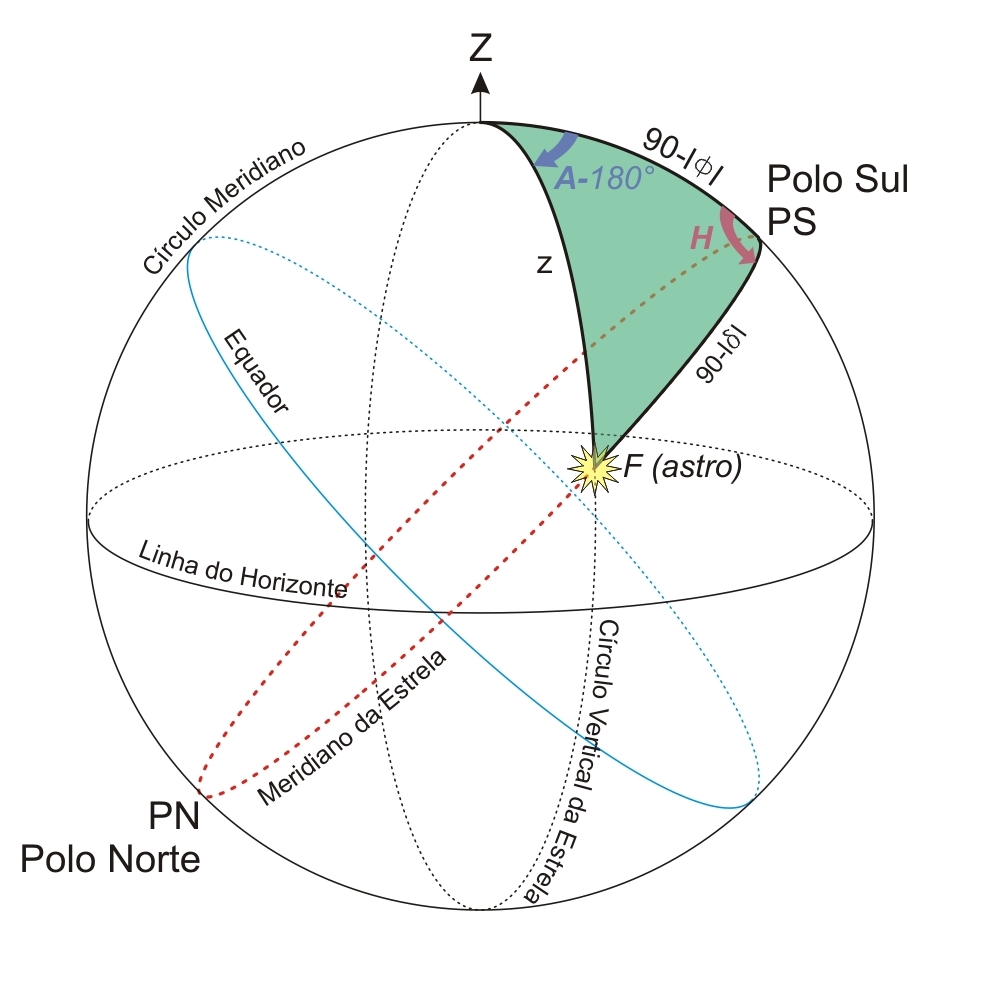
Denomina-se triângulo de posição o triângulo situado na esfera celeste que tem por vértices: o astro, o polo elevado e o zênite.

Os lados e ângulos do triângulo de posição são:

arco entre o zênite e o polo elevado = 90° - |φ|
arco entre o zênite e astro = z
arco entre o polo elevado e o astro = 90° - |δ| (se δ e φ são de mesmo sinal) ou 90° + |δ| (se δ e φ são de sinais contrários)
ângulo com vértice no zênite = A (φ positivo e astro a leste); 360°-A (φ positivo e astro a oeste); A-180° (φ negativo e astro a leste); 180°-A (φ negativo e astro a oeste)
ângulo com vértice no polo elevado = H (astro a oeste) ou 360° -H (astro a leste).
ângulo com vértice na estrela

O triângulo de posição é usado para derivar as coordenadas do astro quando conhecida a posição geográfica do lugar, ou determinar as coordenadas geográficas do lugar quando conhecidas as coordenadas do astro. Também permite fazer as transformações de um sistemas de coordenada para outro (determinar coordenadas do sistema equatorial a partir das do sistema horizontal e vice-versa).

Relações entre distância zenital (z), azimute (A), ângulo horário (H), e declinação (δ)

Usando a fórmula dos cossenos no triângulo de posição podemos tirar duas relações entre os sistemas de coordenadas:

Dedução para δ e φ positivos (caso mais geral do hemisfério norte):

cos z = cos (90° - φ) cos (90° - δ) + sen (90° - φ) sen (90° - δ) cos H = sen δ sen φ + cos δ cos φ cos H
sen δ = sen φ cos z + cos φsen z cos A

Invertendo essas relações para isolar H e A temos:

cos H = cos z sec φ sec δ - tan φ tan δ
cos A = sen δ cosec z sec φ - tan φ cot z

A fórmula dos senos nos dá:
- cos δ / sen A = sen z / sen H

A fórmula dos 5 elementos nos dá:
sen z cos A = cos φ senδ - cos δ sen φ cos H

Dedução para δ e φ negativos (caso mais geral do hemisfério sul):

cos z = cos (90° - |φ|) cos (90° - |δ|) + sen (90° - |φ|) sen (90° - |δ|) cos H
cos (90° - |δ|)= cos z cos (90° - |φ|) + sen z sen (90° - |δ|) cos (A - 180°)

Lembrando que:
cos (90° - |φ|) = sen |φ|= - senφ
cos (90° - |δ|)= sen |δ| = -senδ
sen (90° - |φ|) = cos |φ| = cos φ
cos (A - 180) = - cos A

As equações acima ficam: cos z = sen δ sen φ + cos δ cos φ cos H

e
sen δ = sen φ cos z + cos φsen z cos A

que são idênticas às deduzidas para o hemisfério norte.

Analogamente podemos mostrar que essas fórmulas são válidas para quaisquer valores de latitude e declinação, mesmo com sinais opostos um do outro. Sintetizando, podemos fazer as tranformações de coordenadas entre o sistema equatorial e o sistema horizontal com o conjunto de equações abaixo:

cos z = sen δ sen φ + cos δ cos φ cos H (4)
sen δ = sen φcos z + + cos φ sen z cos A (5)
cos H = cos z sec φ sec δ - tan φ tan δ (6)
cos A = sen δ cosec z sec φ - tan φ cot z ( 7)
- cos δ / sen A = sen z / sen H (8)
sen z cos A = cos φ senδ - cos δ sen φ cos H (9)

Aplicações:

Uma aplicação prática é determinar o ângulo horário de um astro no instante do nascer ou do ocaso, quando sua distância zenital é 90°, pois ele se encontra no horizonte. Da equação (6), obtemos nessa situação:

cos H = cos 90° sec φ sec δ - tan φ tan δ

Como cos 90° = 0, no nascer e no ocaso a fórmula se reduz a
cos H = - tan φ tan δ (10)

Com esta fórmula podemos calcular, por exemplo, quanto tempo o Sol permanece acima do horizonte em um certo lugar e em uma certa data do ano, pois para qualquer astro o tempo de permanência acima do horizonte será 2 vezes o ângulo horário desse astro no momento do nascer ou ocaso.

O azimute do astro no nascer (ou ocaso) também pode ser calculado facilmente usando a fórmula (7), em que temos o azimute em função de δ, z e φ:

cos A = sen δ cosec z sec φ - tan φ cot z

Como cosec 90° = 1 e cot 90° = 0, no nascer e no ocaso a fórmula se reduz a
cos A = sen δ sec φ (11)

Exemplo:

Quanto tempo permanecerá o Sol acima do horizonte em Porto Alegre, cuja latitude é- 30^o, no dia do Solstício de verão no hemisfério sul, em que a declinação do Sol é de -23^o 27'?

Usando a fórmula (10):

cos H = -tan (-30°) tan (-23° 27′) = -0,2504 → H =104,5 ° = 6,966h.

Esse é o ângulo horário do Sol no ocaso, que indica quanto tempo ele fica acima do horizonte após a passagem meridiana. Como um tempo igual já tinha decorrido entre o nascimento e a passagem meridiana, o tempo total que o Sol fica acima do horizonte, nessa data, será

Tempo acima do horizonte= 2 H = 209° ≈ 14 h.

Especificamente, em Porto Alegre, o Sol estará acima do horizonte aproximadamente 14 h e 10 min em 21 de dezembro, e 10 h e 10 min em 21 de junho. Note que a diferença de 10 minutos é devido á definição de que o dia começa com a borda superior do Sol no horizonte, e o dia termina com a borda superior do Sol no horizonte, e não o centro do disco solar, como assumido na fórmula acima.

Os azimutes do Sol no nascer e no ocaso, nessa data, podem ser calculados pela fórmula (11):

cos A = sen δ sec φ
cos A = sen (-23° 27') sec (30°) = -0,46

Logo A = 117°(nascer) ou 243° (ocaso) o que significa que nasce entre o leste e o sul e se põe entre o oeste e o sul.

Efeito da precessão dos equinócios na ascenção reta e declinação

Seja ε = 23,5° a obliquidade da eclíptica, e seja Δλ a variação da longitude eclíptica de uma estrela, pela mudança de posição do ponto Áries de γ para γ₁, devido à precessão do polo de P para P₁.

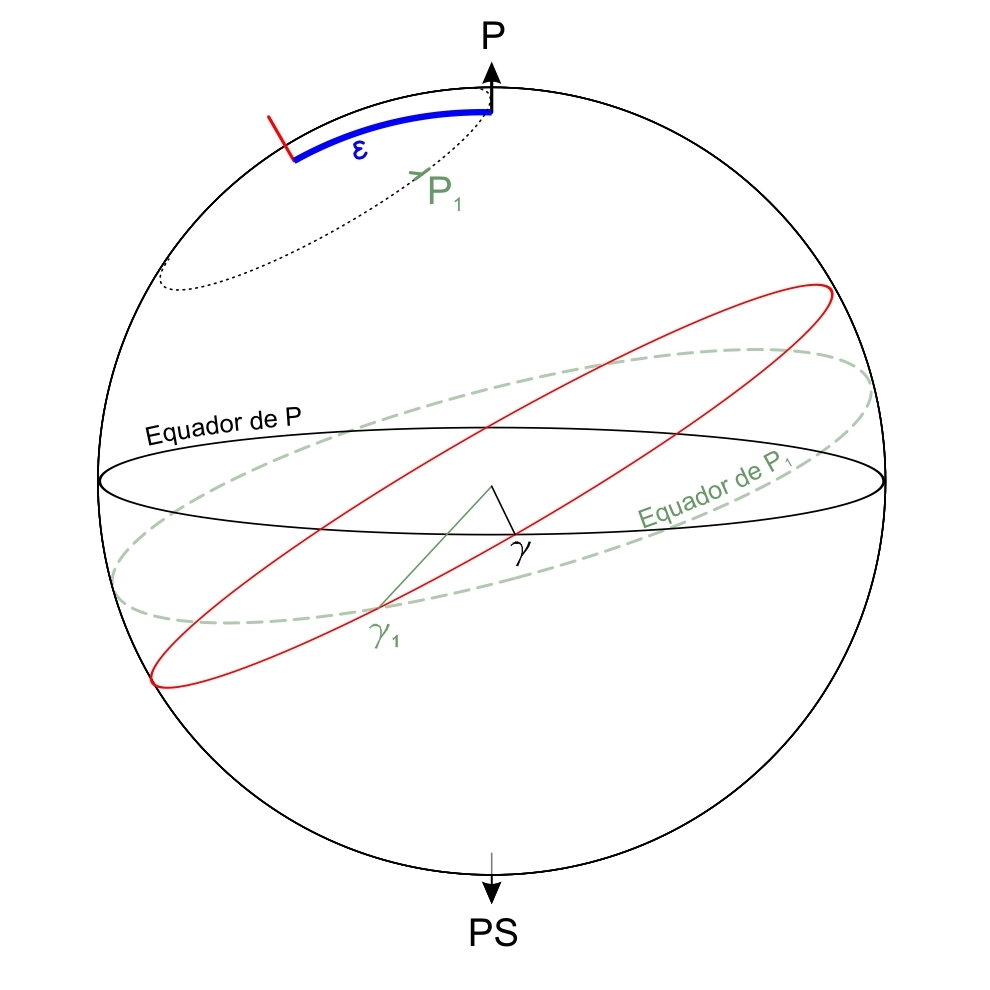
A variação em declinação será:

Δδ = Δλ sen ε cos α
e a variação em acensão reta será: Δα = Δλ(cosε + sen ε sen α tan δ).

Exercícios

Página da disciplin a

Arte das figuras: Adriano Pieres

cos z = sen δ sen φ + cos δ cos φ cos H	(4)
sen δ = sen φcos z + + cos φ sen z cos A	(5)
cos H = cos z sec φ sec δ - tan φ tan δ	(6)
cos A = sen δ cosec z sec φ - tan φ cot z	( 7)
- cos δ / sen A = sen z / sen H	(8)
sen z cos A = cos φ senδ - cos δ sen φ cos H	(9)